To say that I am "gobsmacked" is an understatement! The s(CASP) language fulfills a 40-year-old dream for a computer language that adheres to the "Don’t repeat yourself" philosophy.
s(CASP) was described in 2003 by Joaquin Arias, Manuel Carro, Elmer Salazar, Kyle Marple, and Andgopal Gupta. Constraint Answer Set Programming without Grounding. Here is a recent tutorial published for the language A Short Tutorial on s(CASP), a Goal-directed Execution of Constraint Answer Set Programs. And has been recently implemented in both Caio and SWI-PROLOG. And here is a recent review article s(CASP) + SWI-Prolog = 🔥.
Write your first s(CASP) program using the s(CASP) profile at https://swish.swi-prolog.org.
In this article I’ll describe by way of example, the kind of language that I have been looking for and show a small aspect of what s(CASP) can do that other languages can’t.
Forty years ago, in my undergraduate days, I was introduced to the logic programming language "Prolog". The premise of the language is that a Prolog program captures facts and rules and that Prolog ‘figures out’ how to order the computations required to answer a query. This Prolog Family Relationships example shows how Prolog doesn’t have a preferred direction of computation. The arguments are symmetric with regards to what is known and what is unknown.
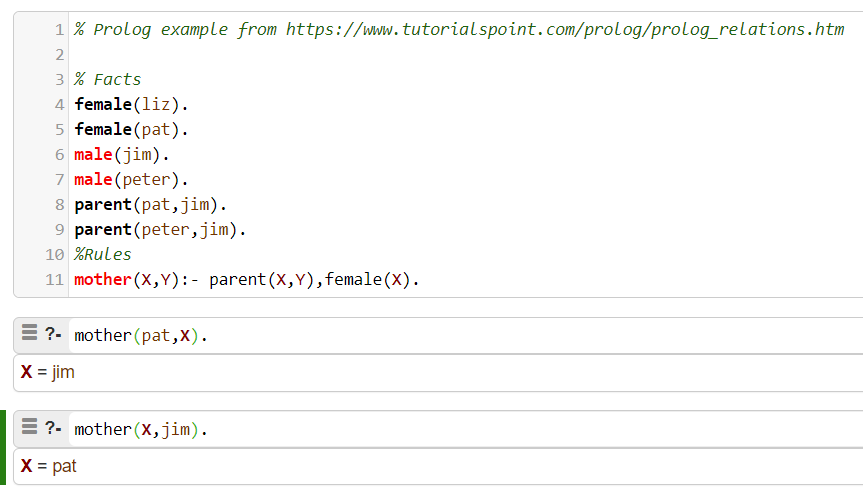
As shown above, if we provide one argument Prolog will compute the other, or if we provide the "other", Prolog will compute the "one".
Dream Computer Language
My dream computer language has, at least, the following capabilities:
- Capture data and computable relationships between data independent of the questions (or queries) that the programmer is currently aware of (unlike procedural languages but like DBMSs do for data)
- Enter information once. For both data and computable relationships and allow any missing data to be computed. Another way of expressing this is that the language handles known and unknown arguments symmetrically, is indifferent to which arguments are known and which are unknown, creating a computation to find the missing arguments (as Prolog does for the computed relationship
mother()and as SQL does for data)
Problem
I soon discovered that Prolog doesn’t keep up its indifference to the direction of computation for long. As soon as mathematical calculations are added to Prolog the paradigm of order-independent facts and rules stops working. Consider the GST in Prolog example Prolog program to calculate a 10% GST (or VAT).
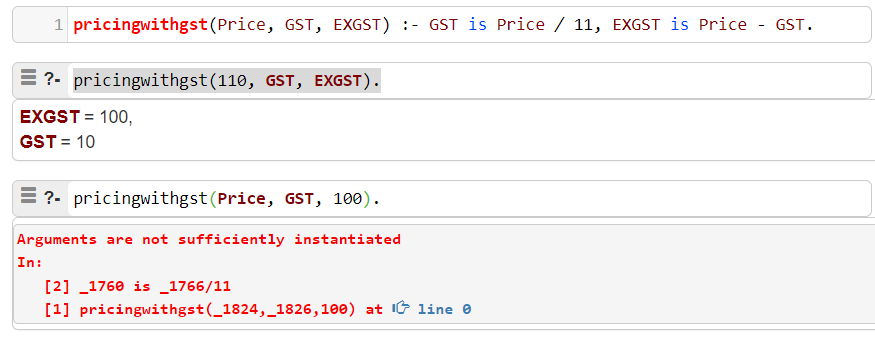
As you can see from the above example, the Prolog language will only find a solution for one direction of computation. While the definition contains enough information to compute both directions to, and from Price, Prolog is unable to do so.
How does s(CASP) compare?
s(CASP) captures the pricingwithgst rule in a similar way to Prolog, but has a ‘super power’ it treats all the arguments to the rule symmetrically and therefore handles the GST example perfectly!
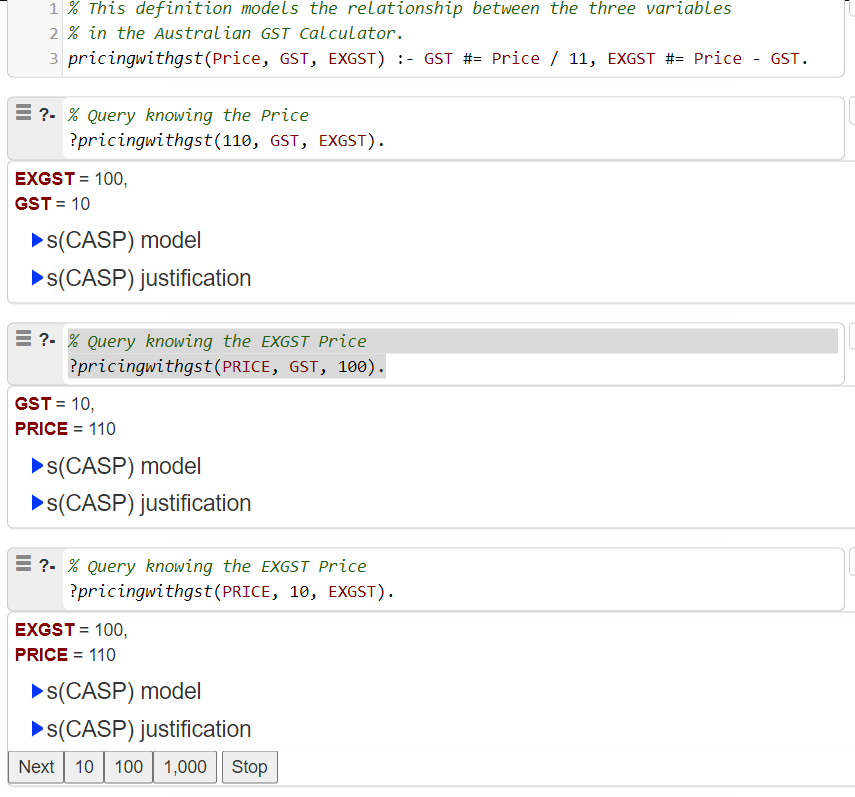
The s(CASP) program contains exactly the same information in the Prolog program and shows the symmetry of handling arguments that I have dreamed of!
Application
A programming language that allows the capturing of a computed relationship (GST being a trivial example) and then doesn’t care which arguments to the relationship are known and which are unknown can reduce the cost of building and maintaining digital models to be used for various purposes.
Following on from the GST example, it is almost certain that the code behind Australia’s GST Calculator web app contains two copies of the computed relationship between Price, GST, and Price exGST, one for each direction of calculation. If s(CASP) was behind the app then the computed relationship would be entered just once as a rule, and the two directions of computation would just be two different queries with different knowns and unknowns. s(CASP) would sequence a computation to find the missing values.